寻找最长回文子串

今日刷题，遇到一道寻找最长回文子串的题。题目给定一个字符串，要求寻找到最长的回文子串长度。

最直接的想法就是暴力求解，即求出每个子串，然后进行判断。但是这个过程实在是太过复杂，求出每个子串的时间复杂度是O(n^2)，判断是否为回文串的复杂度为O(n)，总体时间复杂度为两者相乘O(n^3)。

其次是中心扩展法，让每个字符作为中心向前向后进行匹配。此时时间复杂度为O(n^2)。

动态规划，对于给出的字符串，如果dp[i,j]=1表示系区间的字符串是回文子串，则必定存在dp[i+1,j-1]=1。从而把 该问题化简为一系列子问题可以利用动态规划进行求解了。

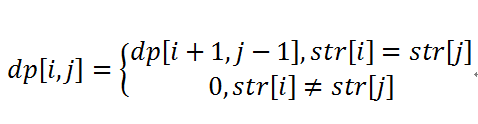
上面状态方程表示，如果s[i]==s[j]且[i+1,j-1]也是回文子串。 但是动态规划的时间复杂度也是O(n^2)。

怎么才能把时间优化下去，是一个很严肃的问题。Google告诉我，有个算法叫做Manacher算法，可以把时间复杂度优化到O(n)。 麻吉代斯噶？ 接下来就学习一下这个马拉车算法。 Manacher首先通过在每个字符串两边都插入一个不可能出现的特殊的符号，将字符串串都转换成奇数（2n+1）例如”aba”变成”#a#b#a#“。 Manacher算法用到一个非常重要的数组Len[i]来表示以s[i]为中心的最长回文子串。

Len[i]数组有一个性质，Len[i]-1就等于该回文串在原串s中的长度

在转换后的字符串s中，所有回文串的长度都是奇数，那么对于以s[i]为中心的最长回文串的长度为2*Len[i]-1, 其中又有Len[i]个分隔符，所以在原字符串中的长度就是Len[i]-1。 接下来看如何求数组Len.

从左往右看，假设0<=j<=i,在计算Len[i]时，Len[j]已经计算过了，设mx为计算过的最长回文串的右端点，id为取得这个端点的位置，则Len[id] = mx - id + 1 . 若i<=mx,找到i相对于id的对称位置，设为j，再次分为两种情况：

• Len[j]<=mx-i

mx的对称点为2*id-mx,i和j所包含的范围是2*Len[j]-i. 说明以j为中心的回文串一定在以id为中心的回文串内部，且i和j关于id对称。 由回文串的定义和对称性，Len[i] = Len[j]。

• Len[j]>mx-i

由对称性说明，以i为中心的回文串可能延伸到mx之外，而大于mx的部分还没有进行匹配，所以要从mx+1处开始逐一匹配，从而更新mx和对应的id以及Len[i]。

若i>mx,说明对于重点为i的回文串一个都没匹配，这时只能一一匹配。匹配完成后更新mx的位置和对应的id以及Len[i]。