快慢指针

1. 有序数组去重复元素

最开始时两个指针都指向第一个数字，如果两个指针指的数字相同，则快指针向前走一步，如果不同，则两个指针都向前走一步

   class Solution {
   public:
       int removeDuplicates(vector<int>& nums) {
           int j = 0, n = nums.size();
           for (int i = 0; i < n; ++i) {
               if (nums[i] != nums[j]) nums[++j] = nums[i];
           }
           return nums.empty() ? 0 : (j + 1);
       }
   };

1. 判断链表是否有环

快指针走两步，慢指针走一步。如果有环，最终快指针会遇上慢指针。

   class Solution {
   public:
       bool hasCycle(ListNode *head) {
           if (!head || !(head->next))
               return false;
           ListNode *fast = head, *slow = head;
           while (fast && fast -> next) {
               slow = slow->next;
               fast = fast->next->next;
               if (fast == slow)
                   return true;
           } 
           return false;
       }
   };

1. 已知链表中含有环，返回这个环的起始位置

   class Solution {
   public:
       ListNode *detectCycle(ListNode *head) {
           //没有思路，看了网上大佬的题解
           //https://www.cnblogs.com/hiddenfox/p/3408931.html
           if (!head || !(head->next)) 
               return NULL;
           ListNode *fast=head, *slow = head;
           while (fast && fast->next ) {
               slow = slow->next;
               fast = fast->next->next;
               if (slow == fast)
                   break;
           }
           if (fast==slow) {
               slow = head;
               while (fast != slow) {
                   slow = slow->next;
                   fast = fast->next;
               }
               return fast;
           } else
           {
               return NULL;
           }
       }
   };

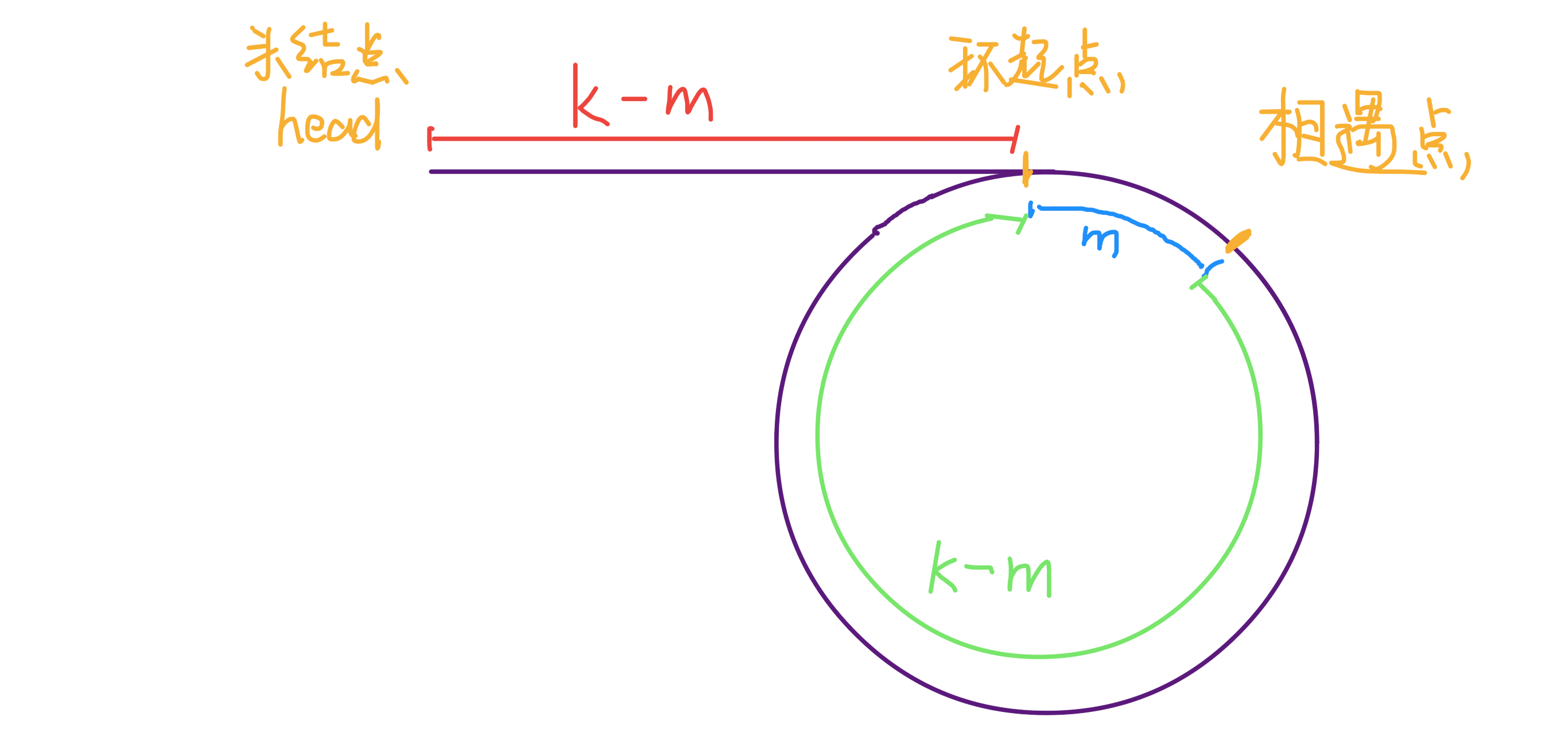
当快慢指针相遇时，让其中任一个指针指向头节点，然后让他俩指向头节点，然后以相同速度前进，再次相遇时所在的节点。

解释：

第一次相遇的时候，假设慢指针走了k步，快指针一定走了2k步，也就是说slow多走了k步，也就是环的长度。

设相遇点距环的起点的距离为 m，那么环的起点距头结点 head 的距离为 k - m，也就是说如果从 head 前进 k - m 步就能到达环起点。巧的是，如果从相遇点继续前进 k - m 步，也恰好到达环起点。

1. 寻找链表的中点

快指针step为2，慢指针step为1。当快指针到达链表尽头时，慢指针处于链表中间。

1. 寻找链表的倒数第k个元素

快指针先走k步，然后快慢指针同速前进。快指针指向null的时候，慢指针指向的就是倒数第k个链表节点。